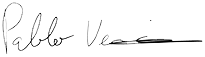Input position (touch or mouse) can be converted back to 3D space by applying unprojection transformation to a 2D device coordinate. This is still problematic, because 3D frustum is squashed into xy-plane and is losing z-component.
Thus, reconstructing full 3D coordinate is not possible without additional step - detecting object intersection etc.
One way of doing it is to have distance to a target object serve as a billboard plane, then:
- using camera FOV, direction and orientation, calculate distances travelled by a pointer as projected onto a plane,
- convert those to a movement around a bounding sphere,
- construct quaternion orientations for origin and destination positions,
- apply constraints as needed (i.e. to make alignment with axis),
- use slerp or other interpolation methods if smooth animation is needed.
Some example code, in Swift:
// Initial 2D device coordinate.
func setStart(point: CGPoint) {
let startCoordWorld = unprojectTouch(point: point)
start = startCoordWorld
next = startCoordWorld
startOrientation = targetNode.simdOrientation.normalized
} // FUNC SET START
// Follow up 2D device coordinate.
func setNext(point: CGPoint) {
let nextCoordWorld = unprojectTouch(point: point)
next = nextCoordWorld
planarToSpherical()
addOrientation = simd_quatf(angle: angleRad, axis: axis).normalized
} // FUNC SET NEXT
// Makes the node change orientation (corresponding to start-next pair).
func jumpToNext() {
targetNode.simdOrientation = (addOrientation * startOrientation)
} // FUNC ORIENT TO NEXT
// Convert viewport point to a world coordinate on an imaginary plane facing camera.
func unprojectTouch(point: CGPoint) -> simd_float3 {
let ndcPoint = viewToNDC(point: point)
let xyPlanePoint = ndcPoint * fovWorldSize * 0.5
// This point is on an imaginary plane that is perpendicular to a view.
let worldPlaneTouchPoint = cameraPos
+ cameraUp * xyPlanePoint.y
+ cameraRight * xyPlanePoint.x
+ cameraFront * distanceCamToPlane
return worldPlaneTouchPoint
} // FUNC UNPROJECT TOUCH
// View coordinates (screen pixels) to NDC (normalized device coordinates).
// Only x and y can be recovered.
func viewToNDC(point: CGPoint) -> simd_float2 {
// Centered in the middle of view.
let x = Float(point.x) - viewportSize.x * 0.5
let y = viewportSize.y * 0.5 - Float(point.y)
let ndc = simd_float2(x * 2.0 / projectionSize,
y * 2.0 / projectionSize)
return ndc
} // FUNC VIEW TO NDC
// Convert plane movement in front of a camera to angular rotation.
// Around "bounding" sphere of a target node.
func planarToSpherical() {
// Plane distance to the sphere center is targetRadius.
let distance = simd_distance(start, next)
angleRad = distance / (targetRadius)
axis = simd_normalize(simd_cross(start, next))
} // FUNC PLANAR TO SPHERICAL
// Intermediate rotation (from current to next).
// Input is normalized in range [0, 1]
func interpolateOrientation(t: Float) {
// slerp has a problem - always takes the shortest arc.
var interOr = simd_bezier(Self.identityOrientation, Self.identityOrientation, addOrientation, addOrientation, t)
interOr = (interOr * startOrientation)
targetNode.simdOrientation = interOr
} // FUNC INTERPOLATE ORIENTATION
Not everything is here, but the general thinking is like that.
To further improve on this - here is an idea - make the orientation snap to predetermined values, like in the following animation :):
Have fun.